Connectivity (graph theory)

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) which need to be removed to disconnect the remaining nodes from each other^[1]. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its robustness as a network.

1 Definitions of components, cuts and connectivity
2 Menger's theorem
3 Computational aspects
4 Examples
5 Bounds on connectivity
6 Other properties
7 See also
8 References

Definitions of components, cuts and connectivity

In an undirected graph G, two vertices u and v are called connected if G contains a path from u to v. Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length 1, i.e. by a single edge, the vertices are called adjacent. A graph is said to be connected if every pair of vertices in the graph is connected.

A connected component is a maximal connected subgraph of G. Each vertex belongs to exactly one connected component, as does each edge.

A directed graph is called weakly connected if replacing all of its directed edges with undirected edges produces a connected (undirected) graph. It is connected if it contains a directed path from u to v or a directed path from v to u for every pair of vertices u, v. It is strongly connected or strong if it contains a directed path from u to v and a directed path from v to u for every pair of vertices u, v. The strong components are the maximal strongly connected subgraphs.

A cut, vertex cut, or separating set of a connected graph G is a set of vertices whose removal renders G disconnected. The connectivity or vertex connectivity κ(G) (where G is not complete) is the size of a smallest vertex cut. A graph is called k-connected or k-vertex-connected if its vertex connectivity is k or greater. This means a graph G is said to be k-connected if there does not exist a set of k-1 vertices whose removal disconnects the graph. A complete graph with n vertices, denoted 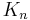$K_n$ , has no vertex cuts at all, but by convention κ( 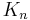$K_n$ ) = n-1. A vertex cut for two vertices u and v is a set of vertices whose removal from the graph disconnects u and v. The local connectivity κ(u, v) is the size of a smallest vertex cut separating u and v. Local connectivity is symmetric for undirected graphs; that is, κ(u,v)=κ(v,u). Moreover, except for complete graphs, κ(G) equals the minimum of κ(u,v) over all nonadjacent pairs of vertices u, v.

2-connectivity is also called biconnectivity and 3-connectivity is also called triconnectivity.

Analogous concepts can be defined for edges. In the simple case in which cutting a single, specific edge would disconnect the graph, that edge is called a bridge. More generally, the edge cut of G is a group of edges whose total removal renders the graph disconnected. The edge-connectivity λ(G) is the size of a smallest edge cut, and the local edge-connectivity λ(u,v) of two vertices u, v is the size of a smallest edge cut disconnecting u from v. Again, local edge-connectivity is symmetric. A graph is called k-edge-connected if its edge connectivity is k or greater.

Menger's theorem

Main article: Menger's theorem

One of the most important facts about connectivity in graphs is Menger's theorem, which characterizes the connectivity and edge-connectivity of a graph in terms of the number of independent paths between vertices.

If u and v are vertices of a graph G, then a collection of paths between u and v is called independent if no two of them share a vertex (other than u and v themselves). Similarly, the collection is edge-independent if no two paths in it share an edge. The greatest number of independent paths between u and v is written as κ′(u,v), and the greatest number of edge-independent paths between u and v is written as λ′(u,v).

Menger's theorem asserts that the local connectivity κ(u,v) equals κ′(u,v) and the local edge-connectivity λ(u,v) equals λ′(u,v) for every pair of vertices u and v.^[2]^[3] This fact is actually a special case of the max-flow min-cut theorem.

Computational aspects

The problem of determining whether two vertices in a graph are connected can be solved efficiently using a search algorithm, such as breadth-first search. More generally, it is easy to determine computationally whether a graph is connected (for example, by using a disjoint-set data structure), or to count the number of connected components. A simple algorithm might be written in pseudo-code as follows:

Begin at any arbitrary node of the graph, G
Proceed from that node using either depth-first or breadth-first search, counting all nodes reached.
Once the graph has been entirely traversed, if the number of nodes counted is equal to the number of nodes of G, the graph is connected; otherwise it is disconnected.

By Menger's theorem, for any two vertices u and v in a connected graph G, the numbers κ(u,v) and λ(u,v) can be determined efficiently using the max-flow min-cut algorithm. The connectivity and edge-connectivity of G can then be computed as the minimum values of κ(u,v) and λ(u,v), respectively.

In computational complexity theory, SL is the class of problems log-space reducible to the problem of determining whether two vertices in a graph are connected, which was proved to be equal to L by Omer Reingold in 2004.^[4] Hence, undirected graph connectivity may be solved in 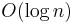$O(\log n)$ space.

The problem of computing the probability that a Bernoulli random graph is connected is called Network reliability and the problem of computing whether two given vertices are connected the ST-reliability problem. Both of these are #P-hard.

Examples

The vertex- and edge-connectivities of a disconnected graph are both 0.
1-connectedness is synonymous with connectedness.
The complete graph on n vertices has edge-connectivity equal to n − 1. Every other simple graph on n vertices has strictly smaller edge-connectivity.
In a tree, the local edge-connectivity between every pair of vertices is 1.

Bounds on connectivity

The vertex-connectivity of a graph is less than or equal to its edge-connectivity. That is, κ(G) ≤ λ(G). Both are less than or equal to the minimum degree of the graph, since deleting all neighbors of a vertex of minimum degree will disconnect that vertex from the rest of the graph.^[1]

For a vertex-transitive graph of degree d, we have: 2(d+1)/3 ≤ κ(G) ≤ λ(G) = d.^[5]

For a vertex-transitive graph of degree d ≤ 4, or for any (undirected) minimal Cayley graph of degree d, or for any symmetric graph of degree d, both kinds of connectivity are equal: κ(G) = λ(G) = d.^[6]

Other properties

Connectedness is preserved by graph homomorphisms.

If G is connected then its line graph L(G) is also connected.

If a graph G is k-connected, then for every set of vertices U of cardinality k, there exists a cycle in G containing U. The converse is true when k = 2.

A graph G is 2-edge-connected if and only if it has an orientation that is strongly connected.

Balinski's theorem states that the polytopal graph (1-skeleton) of a $k$ -dimensional convex polytope is a $k$ -vertex-connected graph.^[7] As a partial converse, Steinitz showed that any 3-vertex-connected planar graph is a polytopal graph (Steinitz theorem).

According to a theorem of G. A. Dirac, if a graph is k-connected for k ≥ 2, then for every set of k vertices in the graph there is a cycle that passes through all the vertices in the set.^[8]^[9]

References

^ ^a ^b Diestel, R., Graph Theory, Electronic Edition, 2005, p 12.
^ Gibbons, A. (1985). Algorithmic Graph Theory. Cambridge University Press.
^ Nagamochi, H., Ibaraki, T. (2008). Algorithmic Aspects of Graph Connectivity. Cambridge University Press.
^ Reingold, Omer (2008). "Undirected connectivity in log-space". Journal of the ACM 55 (4): Article 17, 24 pages. doi:10.1145/1391289.1391291
^ Godsil, C.; Royle, G. (2001). Algebraic Graph Theory. Springer Verlag.
^ Babai, L. (1996). Automorphism groups, isomorphism, reconstruction. Technical Report TR-94-10. University of Chicago. http://www.cs.uchicago.edu/files/tr_authentic/TR-94-10.ps. Chapter 27 of The Handbook of Combinatorics.
^ Balinski, M. L. (1961). "On the graph structure of convex polyhedra in n-space". Pacific Journal of Mathematics 11 (2): 431–434. http://www.projecteuclid.org/Dienst/UI/1.0/Summarize/euclid.pjm/1103037323.
^ Dirac, Gabriel Andrew (1960). "In abstrakten Graphen vorhandene vollständige 4-Graphen und ihre Unterteilungen". Mathematische Nachrichten 22: 61–85. doi:10.1002/mana.19600220107. MR 0121311 .
^ Flandrin, Evelyne; Li, Hao; Marczyk, Antoni; Woźniak, Mariusz (2007). "A generalization of Dirac's theorem on cycles through k vertices in k-connected graphs". Discrete Mathematics 307 (7–8): 878–884. doi:10.1016/j.disc.2005.11.052. MR 2297171 .